Intro to Assembly
The language of machines can be understood by anyone. Sometimes, the only way to truly understand what your machine is doing, is to listen to that language. Romhacking, reverse-engineering, optimized code, and glitch-hunting are just a handful of the uses of learning Assembly language. By the end of this guide, you'll be able to read the ARM Assembly language, and will also have a solid grasp of the most fundamental inner workings of machines.
Binary
The total number of unique symbols needed to encode all of the information known to mankind, is 2. In 1689, the renowned mathematician and philosopher Gottfried Leibniz invented binary. He outlined the rules of binary arithmetic. 200 years later, with the rise of the era of electricity, came the realization that the entirety of binary logic and arithmetic could be expressed by flipping electrical switches on and off.
Binary is a counting system, containing only two symbols: 0 and 1. Decimal is another counting system, containing ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. A counting system with n symbols is called a "base n" counting system (binary is "base two", decimal is "base ten").
To represent numbers larger than the largest symbol, we combine symbols.
Counting in decimal can be reduced to just two rules:- increment the rightmost symbol by 1
- to increment the symbol 9, reset it to 0, then increment the symbol to its left
Because of these rules, the symbol 10 in decimal represents ten groups of 1, 100 represents ten groups of 10, 1000 represents ten groups of 100, etc. In general, any symbol S followed by n zeroes represents S*(10^n)
In binary, we do exactly the same thing. To increment the symbol 1, we reset it to 0, then increment the symbol to its left.
In binary, the symbol 10 represents two groups of 1, 100 represents two groups of 10, 1000 represents two groups of 100, and so on.
To generalize: any symbol S followed by n zeroes reperesents S*(2^n).
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
We can deduce the total quantity represented by any binary number by adding up the quantities that each digit represents.
Example:110101
1 1 0 1 0 1 //The binary digits, aka "bits", spread out
1*(2^5) + 1*(2^4) + 0*(2^3) + 1*(2^2) + 0*(2^1) + 1*(2^0) //Replace with the quantities they represent
32 + 16 + 0 + 4 + 0 + 1 = 53
so 110101 in binary is 53 in decimal.
It will help to memorize powers of 2
| 2^0 = 1 |
| 2^1 = 2 |
| 2^2 = 4 |
| 2^3 = 8 |
| 2^4 = 16 |
| 2^5 = 32 |
| 2^6 = 64 |
| 2^7 = 128 |
| 2^8 = 256 |
| 2^9 = 512 |
| 2^10 = 1024 |
To convert a decimal number to binary, it's easiest to try to construct your binary number one digit at a time, from left to right, using the following method:
- find the largest power of 2 that will fit inside of the total number
- subtract that power of 2 from the total
- repeat the process on what remains
- for the answer, write 1's in positions corresponding to the powers of 2 you used, and 0's elsewhere
Example:
53
53 - 2^5 = 21 //Subtract 2^5 (2^6 is too big)
21 - 2^4 = 5
5 - 2^2 = 1
1 - 2^0 = 0
Result: 2^5 + 2^4 + 2^2 + 2^0 = 110101
To add and subtract binary numbers, use the same methods you use in decimal:
- add/subtract digit by digit, from right to left
- if adding, carry a 1 if the previous digits add up to more than 1
- if subtracting, borrow a 1 if you have to subtract a 1 from a 0
Even multiplication and division use the same methods as decimal, and it's easier in binary. (I won't go into detail here though). If you must, then you can always convert to decimal first, perform the operation, then convert back to binary.
So why is this useful? With electricity, we can use a high voltage to represent 1, and a low voltage to represent 0. By utilizing on and off switches, it is possible to combine those voltages in ways that exactly mimic all of binary arithmetic. The ability to convert between binary and decimal bridges the gap between the computational capabilities of electrical circuits, and the math we learned in grade school. With this knowledge, we can create machines to perform that math at the speed of light. This series will cover exactly how that's done.
Other Bases
Hexadecimal is a counting system containing 16 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
The great thing about hexadecimal is that it's extremely easy to convert between it and binary, plus it's easier for humans to read! To convert from hex to binary, you can convert each digit individually to binary, then stick all of the binary digits together.
DA2F
D = 1101
A = 1010
2 = 0010
F = 1111
DA2F = 1101 1010 0010 1111
Why that works:
In hexadecimal, any symbol S followed by n zeroes represents S*(16^n). 16^n is the same as 2^(4n). For this reason, appending a 0 to a hex number (increasing n by 1) is the same as appending four 0's to its binary form; each process multiplies the number by 16. For example, B in hex is 1011 in binary, while B0 in hex is 10110000 in binary. To deduce the binary quantity of a hex number, we can again add up the quantities that each digit represents. In the example above, DA2F, we can think of it as D000 + A00 + 20 + F. D000 in binary would be 1101 0000 0000 0000, A00 would be 1010 0000 0000, 20 would be 0010 0000, and F would be 1111. Adding them up gives the same result as the example above.
| Hexadecimal | Binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Just like the other counting systems, to count past the last symbol, you reset it to zero, then increment the symbol to its left. ...D, E, F, 10, 11, 12.... To avoid ambiguity, hexadecimal numbers are usually prefixed with "0x", which just means "the following number is hexadecimal". ...0xD, 0xE, 0xF, 0x10, 0x11, 0x12....
You may also encounter "octal", which is a base 8 counting system. Similar to hexadecimal, it is easy to convert to and from binary, the only difference being that each octal digit is allocated 3 binary digits instead of 4.
Terminology and Usage
A single digit in binary is called a bit. Bits are often used to represent on/off, or true/false. Bits are also used to represent integers, letters, and other symbols. In modern computers, the smallest addressable units of memory, or bytes, each contain 8 bits. With 8 bits, you can represent any number from 0 to 255 (00000000 to 11111111). In a basic text document, English letters are represented with one byte each, translated using the ASCII table.
For any binary value, the least significant bit (lsb) is the rightmost bit, and the most significant bit (msb) is the leftmost bit. To refer to a specific bit in a value, we number each bit from right to left, starting at 0. The lsb is bit 0, the bit to the left of that is bit 1, left of that is bit 2, left of that is bit 3, etc.
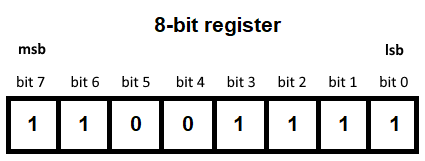
Registers are tiny containers of bits. Bytes are typically contained within 8-bit registers. Math done between registers is similar to math done with normal binary, except that any overflowed/underflowed bits are just dropped, swallowed by the void.
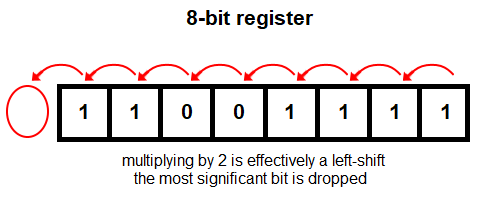
For example, suppose you have an 8-bit register with the value 11001111. To multiply it by 2, we shift each digit to the left: 110011110. But in bit-shifting left, the number no longer fits within 8 bits, so the most significant bit (msb) is dropped, or "shifted out". What remains inside the register is 10011110. Similarly, if we divide by 2, we shift each digit to the right and the least significant bit (lsb) is shifted out. Any vacated bits are automatically filled with 0.
This has an interesting side effect: 11111111 + 1 = 100000000, which becomes 0 because the msb doesn't fit inside the 8-bit register. This effect is called "rolling over", meaning that the operation passed the max value, and landed on or crossed over 0. Conveniently, this allows us to express negative numbers in registers.
Negative Numbers
The defining property of negative numbers is that when added to their positive counterparts, they result in 0
x + -x = 0
To express -1 in an 8-bit register, you would actually use 11111111, because when you add 1 to that, it rolls over to 0. To express -1 in a larger register, you'd need to fill the whole register with 1s. A useful shortcut for finding the negative of a number is to toggle every bit, then add 1.
Why not just use a negative sign? The negative sign is a symbol. It's another form of information. Remember, our register can only store information using 2 symbols, 0 and 1, aka low or high voltage. While it is possible to use a separate register for each number to represent positive/negative, that method is far less efficient, and more difficult to hard-wire into a computer chip. Note that 11111111 means either 255 or -1 in an 8-bit register. Which way to interpret it is based purely on context.
At the physical level, a 1-bit register is made up of an electrical circuit containing just a handful of electrical switches (transistors) in a very clever arrangement. This circuit has the ability to store an electrical signal, and output it continuously, until the signal is overwritten, or the computer is turned off. It will be covered in the next lesson.